Simple MCMC in R
Here's an ultra-basic Metropolis-Hastings sampler implemented in R, for illustrative purposes:
metropolis1<-function(n, a, b)
{
sim<-numeric(n)
sim[1]<-x<-0
for (i in 2:n) {
prob=runif(1,a,b)
cand=x+prob
ratio=min(1,dnorm(cand)/dnorm(x))
u=runif(1)
if (u < ratio)
x=cand
sim[i]=x
}
sim
}
par(mfrow=c(1,1))
res<-metropolis1(1000,-1, 1 )
plot(res, type="l", col="dark red")
IRL, you'd want to convert to log-likelihood to avoid potential numeric underflow.
Here's a worked example with two unknown parameters. Say we have a sample $X$ that we suspect is drawn from a normal distribution: $X \tilde{} N(\mu, \sigma^2)$. So, $\mu$ and $\sigma$ are unknown random variables. Let's assume uninformed Gaussian priors:
- $\mu \tilde{} N(0,10^2)$
- $\sigma \tilde{} N(0,10^2)$
Now let's specify the likelihood function, then the MCMC sampling code, and finally generate some random data and do MCMC on it:
# log-likelihood function
# theta is 2-value vector: mu and sigma
loglikelihood<-function(theta, mdata){
mu<-theta[1]
sigma<-theta[2]
n<-length(mdata)
# calculate probabilities of each X given mu & sigma
zz = dnorm(mdata, mean=mu, sd=sigma)
# cannot log 0's so replace with tiny positive value
zz[zz<=0] = 1e-16
# calculate & return log-likelihood
sum(log(zz))
}
# mcmc function
mcmcevd<- function(nn, init, std, mdata, burn) {
theta<-init
simmat<- matrix(NA, nn+1, ncol=length(theta))
colnames(simmat) <- c("mu","sigma")
simmat[1,]<-init
acc.counts<-numeric(2)
llikelihood.old<-loglikelihood(theta, mdata)
for(i in 1:nn){
## mu
# calculate posterior probability using current beta1
logposterior.old<-llikelihood.old+dnorm(theta[1], sd=100, log=TRUE) #likelihood * prior = logLikelihood + log(Prior)
# record current beta1
mu.old<-theta[1]
# generate proposal for beta 1
mu.new<-rnorm(1, mu.old, std[1]) #Simulating a value from a normal distribution
# write proposal to theta vector
theta[1]<-mu.new
# calculate log-likelihood using new theta vector
llikelihood.new<-loglikelihood(theta, mdata)
# calcualte posterior using new beta1
logposterior.new<-llikelihood.new+dnorm(theta[1], sd=100, log=TRUE) #Prior and logLikelihood
##DECISION WHETHER REJECT/ACCEPT
alpha<- min(exp(logposterior.new-logposterior.old),1)
u<-runif(1,0,1)
if(alpha > u)
{
simmat[(i+1),1]<-mu.new
acc.counts[1]<-acc.counts[1]+1
llikelihood.old<-llikelihood.new
}
else
simmat[(i+1),1]<-mu.old
theta[1]<-simmat[(i+1),1]
## sigma
# this is special: cannot have negative value,
# so we draw from LOG-NORMAL.
# This is not a symmetric distribuiton
# so we need special non-symmetric component in accept/reject
sigma.old<-theta[2]
sigma.new<-exp(rnorm(1,log(sigma.old),std[2])) #Simulating a value from a lognormal distribution
theta[2]<-sigma.new
llikelihood.new<-loglikelihood(theta, mdata)
logposterior.new<-llikelihood.new+dnorm(theta[2], sd=10, log=TRUE) #Prior and logLikelihood
##DECISION WHETHER REJECT/ACCEPT
nonsymm<-log(sigma.new/sigma.old)
alpha<- min(exp(logposterior.new-logposterior.old+nonsymm),1)
u<-runif(1,0,1)
if(alpha > u)
{
simmat[(i+1),2]<-sigma.new
acc.counts[2]<-acc.counts[2]+1
llikelihood.old<-llikelihood.new
}
else
simmat[(i+1),2]<-sigma.old
theta[2]<-simmat[(i+1),2]
} ##End of simulation loop
simmat<-simmat[(burn+1):nn,]
acc.rates<-c(acc.counts)/nn
list(simmat=simmat, acc.rates=acc.rates)
} #End of Function
# generate some random data
mdata<-rnorm(25, 5, 2)
# do MCMC
init<-c(1, 1) # specify initial values for mu & sigma
std<-c(1, 0.5) # specify standard deviation for "step size"
xx<-mcmcevd(nn=20000, init, std, mdata=mdata, burn=2000)
## Results
xx$acc.rates # print accept rates
# print chain & histogram distributions
temp<-xx$simmat
par(mfrow=c(2,2))
plot(temp[,1], type="l")
plot(temp[,2], type="l")
hist(temp[,1])
hist(temp[,2])
# print mean posterior point estimates
mean(temp[,1])
mean(temp[,2])
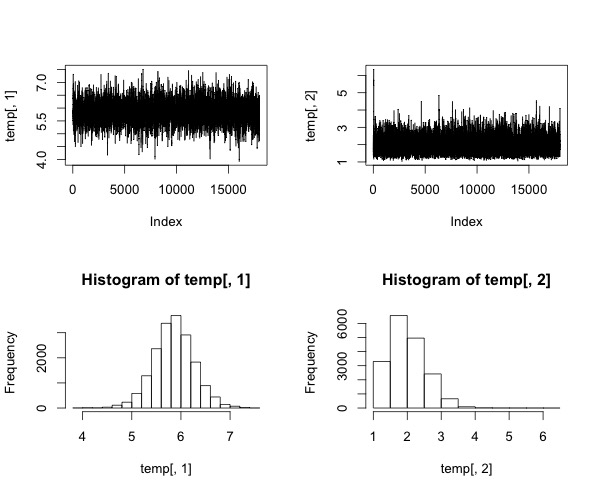
Notice that for sigma we draw samples from the log-normal distribution. That's because sigma cannot be negative.
There are hyperparameters that must be fiddled with to ensure that the sampling happens correctly, the chain converges, etc.:
- The burn-in period
- The length of the sample
- The 'step size' - that is, standard deviation of the distribution used to generate new values. One should aim to get ~50% of steps accepted.